PCA를 할머니한테 설명할 수 있니?

학부 시절, 다변량통계분석 수업 교수님께서 우리한테 그랬다. “PCA를 할머니가 이해할 수 있도록 설명해줄 수 있어요? 설명을 학교 웹사이트에 올리면, 그 사람은 A+ 을 줄게요.”

나는 그렇게 겸허히 B+을 받았다.

솔직히 말하면 그 당시에는 PCA 에 대해 제대로 이해하지 못하고 있었다. 지금은… 지금도 100% 이해했다고는 말 못하겠다. 그러다 어느날 cross validated 를 구경하다가 이 정도 설명이면 완벽하다고 봐도 되지 않을까 싶은 글이 올라와서 해당 글을 한국어로 번역해보도록 하겠다. (의역이 많고 오역도 있을 수 있으니 혹시나 발견하면 댓글로 꼭 지적해주세요) 원문은 아래 링크에서 가장 많은 vote를 받은 답변이다. 제목을 클릭하면 원문으로 이동한다. 설명 중간 중간에 있는 이미지들을 그대로 가져왔는데, 문제시 삭제하도록 하겠다.

---

Making sense of principal component analysis, eigenvectors & eigenvalues

가족들이 모두 모인 식사자리에서 사람들이 당신에게 PCA 에 대해 물어보기 시작했다. 먼저 증조할머니에게 설명드린 다음에 할머니에게, 그리고 엄마에게, 부인에게, 그리고 마지막으로 수학을 전공한 당신의 딸에게 순서대로 설명해보도록 하자. (…장유유서가 여기서?) 그러니까 점점 ‘덜 비전문가’ 인 사람에게 설명하게 되는 것이겠다. 대화는 이런 식일 것이다.

증조할머니: 너 피씨에인가 뭐시긴가 공부한다던데, 그게 대체 뭐니?

당신: 아, 그러니까 그건 어떤 정보를 요약하는 방법이에요. 예를 들어, 여기 술병 몇개가 식탁 위에 있잖아요? 얘네들을 각각 색깔, 도수, 몇년산인지 등등으로 설명할 수 있겠죠. 우리 집에 있는 모든 술을 이런 수많은 특성들로 표를 만들어서 정리할 수 있을 거예요. 근데 어떤 특성들은 서로 관련이 있을테니까 결국 중복된 내용이 있게 되는거겠죠? 이런 중복된 것들은 요약해서 더 적은 특성으로 술들을 설명하는 방법이예요.

할머니: 그거 참 신기하구나. 그래서 그 PCA 라는 거는 어떤 게 중복되는지 확인해서 그걸 없애버리는 거니?

당신: 할머니, 좋은 질문이에요. PCA 는 특성들을 골라내고 나머지를 버리는 방법은 아니에요. 대신 이 술들을 잘 설명할만한 새로운 하나의 특성을 만들어내죠. 당연히 이 새로운 특성은 기존에 리스트에 있던 특성들을 이용해서 만들어져요. 예를 들어, 새로운 특성은 술의 숙성기간에서 산미의 정도를 뺀다거나, 뭐 그런식으로 두 개를 이리저리 조합해서 만들어질 수 있어요. (이걸 우리는 선형 결합이라고 해요.)

사실, PCA는 가능한 가장 최선이자 모든 선형결합 중 유일하게 가능한 특성들을 찾아내요. 그래서 쓸 만 한 거죠.

엄마: 으음, 되게 좋은 방법으로 들리긴 하는데, 난 솔직히 내가 제대로 이해했는지 모르겠어. 새로운 PCA 특성들이 술들의 특성을 “요약” 한다는게 무슨 말이야?

당신: 여기에는 두 가지 답변을 드릴 수가 있겠네요. 하나는, 우리가 술들 간에 확연히 차이가 나는 특성을 찾고 있다는 거예요. 만약에 우리가 모든 술들이 거의 비슷하게 가지고 있는 특성을 찾아냈다고 생각해보면, 이건 그렇게 유용하지 않겠죠? 술들은 서로 되게 다른데, 그 특성만 보면 모두 똑같은 술이라고 생각하게 될테니까요. 이건 나쁜 요약이에요. 대신 PCA 는 술들간의 차이를 확연하게 보여주는 특성들을 찾아내요.

두번째는, 우리는 원래의 술들을 예측하거나 재구성할 수 있도록 하는 특성들을 찾고 있다는 거예요. 우리가 술들에 대해 알고 있던 기존의 특성들과 완전히 관계 없는 특성을 찾아냈다고 생각해봐요. 우리가 만약에 이 특성을 사용해서 술을 설명하게 되면, 기존의 특성들에 대해서는 전혀 설명할 수 없게 되죠. 이것도 나쁜 요약이 돼요. 그래서 PCA 는 기존에 우리가 알고 있던 특성들을 잘 재구성할 수 있도록 하는 특성들을 찾아내요.

그리고 놀랍게도 이 두가지 목표는 사실 같은 것이고, PCA를 사용해서 일석이조의 효과를 누릴 수가 있는 거예요.

아내: 근데 여보! 두개는 전혀 다르게 들리는걸? 어떻게 두개가 같은건데?

당신: 흠, 그림을 하나 그려볼까. 술의 특성 두가지를 생각해보자. 술 색깔의 진한 정도랑… 알콜도수라든지? 둘이 상관관계가 있는지는 잘 모르겠지만 있다고 치자고. 그럼 술들의 산점도는 이렇게 그려질거야.

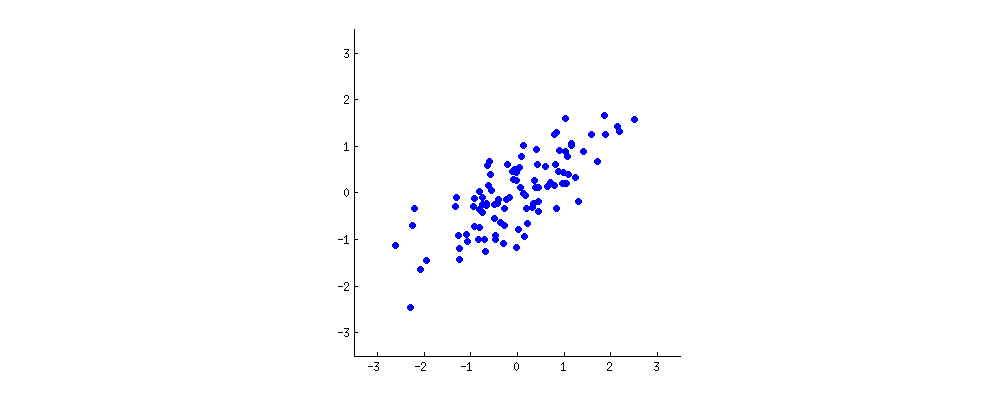
이 뭉게구름같은 그림의 점 한개는 술 한개를 뜻해. 가로축의 특성과 세로축의 특성은 서로 상관관계가 있어 보이지. 새로운 특성은 이 뭉게구름의 가운데를 뚫고 지나가는 선을 그린 다음 그 선에 모든 점들을 영사하는 방법으로 만들어 질 수도 있을거야. 새로운 특성은 $w_1 x + w_2 y$ 와 같이 선형 결합으로 나타낼 수 있을거야.

잠시 영사가 뭔지 모르는 분들을 위해 설명고자의 설명 : 영사(projection)는…. 그림자 놀이입니다. 나는 3차원에 있지만 그림자는 2차원의 벽에 존재하잖아요? 나랑 내 동생이 서서 햇빛 쐬고 있으면 그림자도 벽에 두 개가 생길겁니다. 그러니까 저랑 제 동생을 직접 안봐도 위치를 대충 그림자 보고 짐작할 수 있겠죠? 뭐 그런 겁니다. 설명고자라 죄송해요…. 나중에 더 좋은 설명을 생각해보겠습니다.

자 여기 잘 봐봐, 선(특성)이 어떻게 그어지냐에 따라 어떻게 영사가 달라지는지.

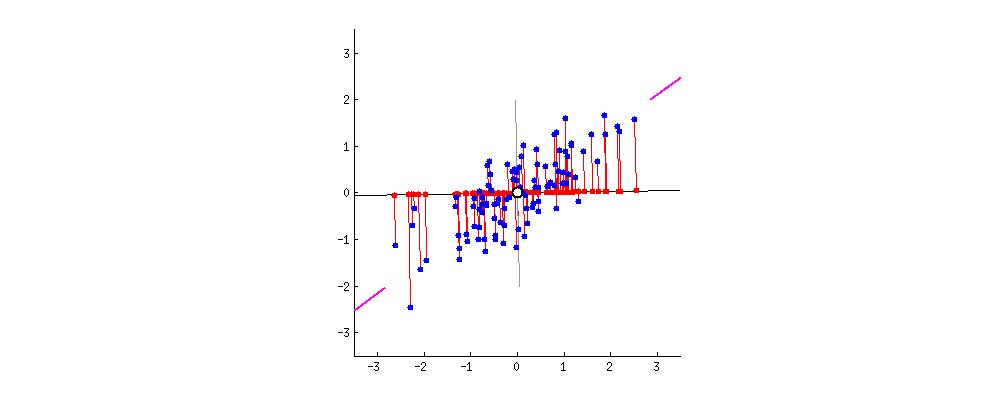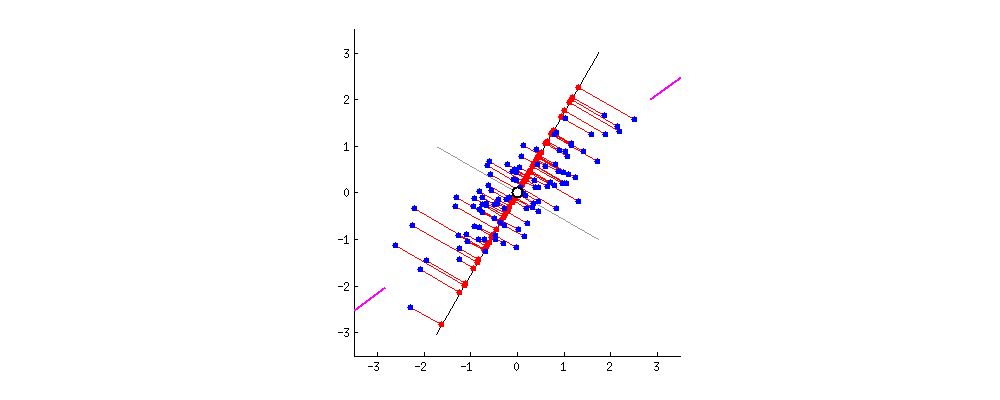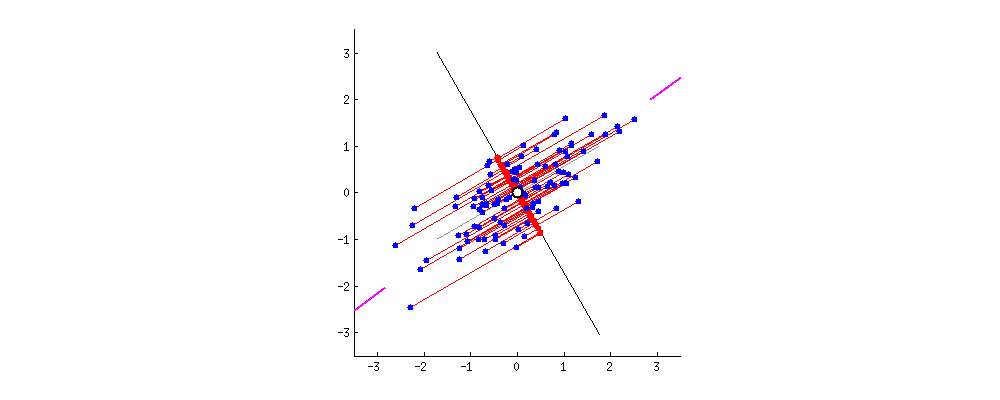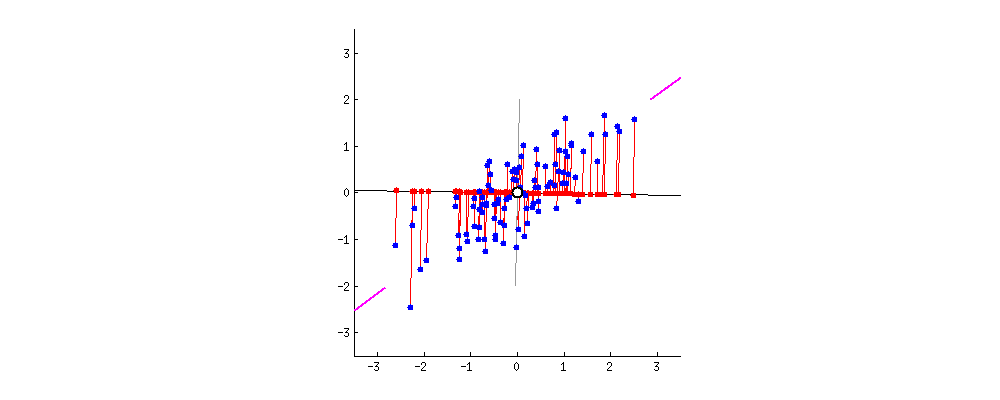
아까 말했듯이 PCA 는 두 가지 기준에 따라 뭐가 제일 좋은 선인지 판단할 거야. 먼저, 선 위로 영사되는 값들의 분산은 가장 커야겠지. 위 그림에서 선이 돌면서 빨간 점들이 퍼지는 정도가 어떻게 달라지는지 봐. 언제 가장 많이 퍼져있는지 보이지? 그리고 두번째, 만약에 우리가 새로운 특성에서 원래의 두가지 특성을 재구성한다면 (즉, 빨간 점에서 다시 파란 점으로 돌아가려면) 재구성 할 때 생기는 오차는 빨간 점과 파란 점 간의 거리 즉, 저 그림에서는 빨간 선의 길이가 될거야. 저 빨간 선들의 길이의 합이 언제 가장 작아지는지도 보이지?

저 움직이는 그림을 좀 보고 있다보면, ‘최대분산’ 과 ‘최소오차’ 가 동시에 만족되는 시점이 있다는 걸 알게 될거야. 내가 진분홍 색으로 끝을 표시해 둔 선 말이지. 그 때의 선이 PCA 가 찾아낸 새로운 술의 특성이 되는거야.

아, PCA 는 ‘principal component analysis(주성분분석)’ 의 준말이고, 이 새로운 특성은 ‘첫번째 주성분’ 이라고 불러. 그리고 지금까지 불러왔던 것처럼 특성(property or characteristic)이라고 부르는 대신 우리는 이걸 보통 특징(feature) 이나 변수(variable) 이라고 부르지.

딸: 아빠 좀 멋지다ㅎㅎ 나 왜 두가지 목표가 하나의 결과를 내는지 알 거 같아. 피타고라스 이론 때문 아니야? 아무튼 나는 PCA 가 고유벡터랑 고윳값에 관련이 있다고 들었어. 아빠가 그린 그림에 얘네도 그려져있는거야?

당신: 관찰력이 좋구만. 수학적으로 빨간 점들이 흩어진 정도는 뭉게구름 가운데에서부터 빨간 점 사이의 거리 제곱들의 평균이지. 너가 알고 있듯이, 이건 분산이라고 불러. 근데 재구성했을 때의 총 오차는 그림에서의 빨간 선들의 제곱들의 평균이야. 근데 검은 선이랑 빨간 선 간의 각도는 언제나 직각이니까, 두가지의 합은 뭉게구름 가운데에서부터 파란 점 사이의 거리의 제곱의 평균과 같아지게 돼. 너가 말했듯 피타고라스 이론에 의해서지. 이 평균값은 당연히 선의 위치와는 관계없이 일정하기 때문에, 분산이 높아질 수록 오차는 작아지겠지.

검은 선이 단단한 막대기고, 빨간 선은 스프링이라고 상상해보자. 스프링의 힘은 길이 제곱에 비례하니까 (이걸 물리학에서 훅 법칙이라고 해.) 막대기는 스스로 이 길이 제곱의 합들을 줄이는 방향으로 향하게 될거야. 점성 마찰을 추가해서 시뮬레이션해보면 이렇게 돼.

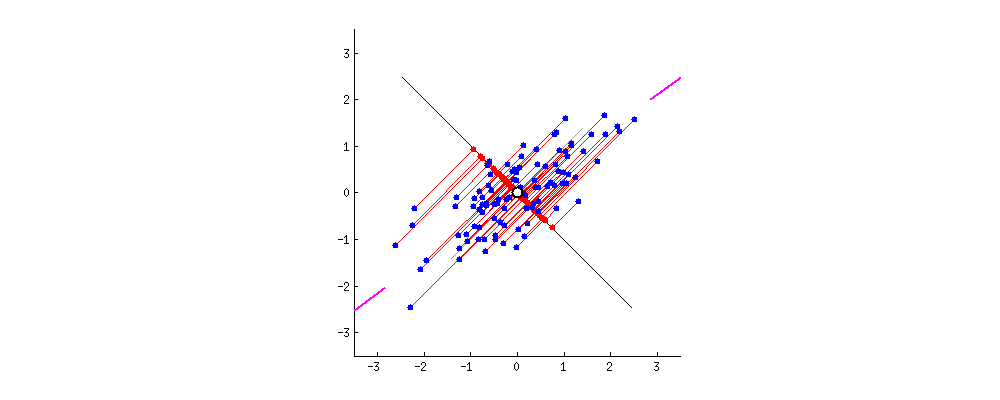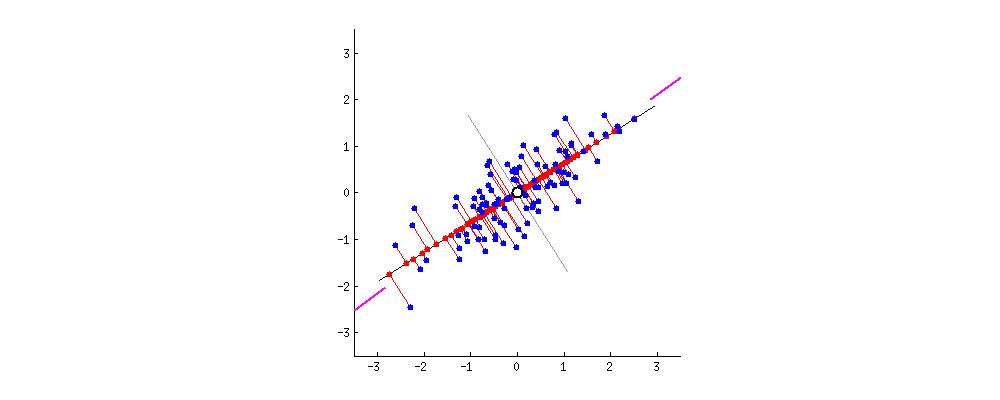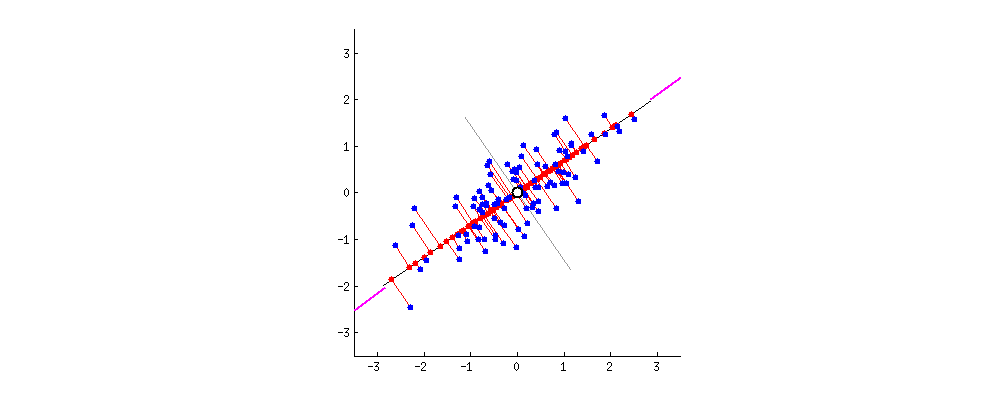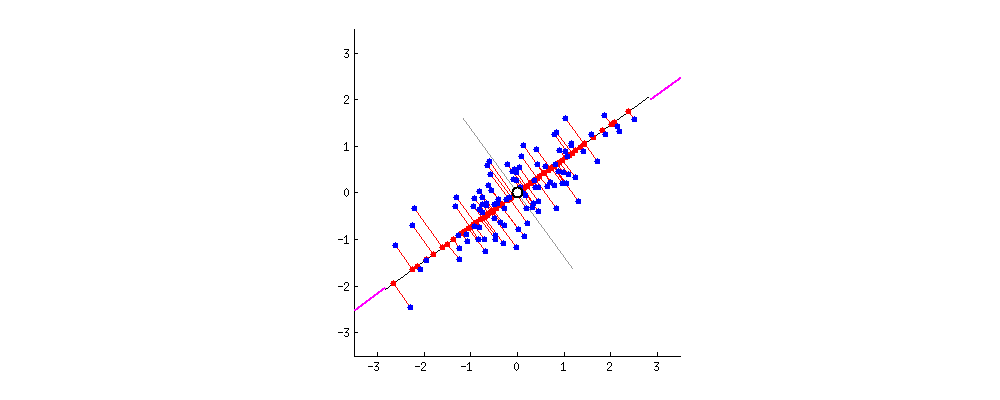
고유벡터와 고윳값에 대해 생각해보자. 공분산행렬이 뭔지는 알거야. 내 예시에서 사용할 예시 행렬은 아래의 $2 \times 2$ 행렬이야.

\[\begin{pmatrix}1.07 &0.63\\0.63 & 0.64\end{pmatrix}\]

그러니까 x의 분산은 1.07, y의 분산은 0.64, 둘의 공분산은 0.63 이라는 말이지. 정사각 대칭행렬이니까 이 녀석의 고유벡터로 주어진 새로운 직교좌표계를 채택해서 얘를 대각행렬로 만들어 줄 수 있을거야. 대각행렬의 대각에 위치한 값들은 해당하는 고윳값들일거고. 이 새로운 좌표계에서 공분산행렬은 대각행렬이고 이렇게 생겼어:

\[\begin{pmatrix}1.52 &0\\0 & 0.19\end{pmatrix}\]

즉 둘 간의 공분산은 이제 0이라는거지. 어떤 영사의 분산이더라도 고윳값의 가중평균으로 주어질 거란 게 분명해졌어. 그리고 이에 따라, 가능한 최대의 분산 (1.52) 는 우리가 첫번째 좌표축에 영사를 했을 때 이루어지겠지.

이건 아까 보여줬던 그림에서도 볼 수 있어. 검은 선과 직교하는 회색 선이 있잖아. 얘네 둘이 좌표계를 이루는거지. 이 좌표계를 기준으로 언제 파란 점들이 상관관계가 없어지는지 봐봐. 정답은 또 검정 선의 양 끝이 진분홍색 선에 닿을 때가 될거야. 이제 내가 저 진분홍색 선의 위치를 어떻게 찾았는지 말해줄 수 있겠구나. 진분홍색 선은 공분산행렬의 첫번째 고유벡터의 방향, 그러니까 이번 예시에서는 $(0.81,0.58)$을 표시한 거란다.