Quantile Regression

한 달 전에 어찌저찌 얼렁뚱땅 논문 본심이 끝나고, 나는 드디어 대학원을 졸업하게 되었다. 당시 통과된 내 학위논문은 Quantile Regression (분위회귀분석), 특히 Censored data 에 대한 Quantile Regression 에 대한 것이다. 나의 무사 졸업을 기념하면서 블로그에 Quantile Regression 에 대해서 간단히 적어볼까 한다.

1. Quantile

우선 Quantile 이 무엇인지부터 알아야한다. 총 100명의 학생이 시험을 쳤는데, 그 중에 상위 25등을 한 학생의 점수를 우리는 ‘0.75th quantile’ 이라고 하고, Q(0.75) 라고 표기한다. 같은 말을 수식으로 나타내보자. 아무 real valued random variable Y 에 대하여 cumulative distibution function 을 F(y) 라고 하자. 어떤 $0<\tau<1$ 에 대해서

\[\begin{aligned} Q(\tau) = \inf \{ y : F(y) \ge \tau \} \end{aligned}\]

로 표현할 수 있다.

2. Recall : Linear Regression

사실 나는 Quantile Regression 을 처음에 공부할 때 뭔가 와닿지가 않아서(?) 원래 알고 있던 Linear Regression 과 비교하며 생각하곤 했다. Linear Regression 을 복습해보자. Linear Regression 에서는 아까의 random variable Y 에 대하여 이러한 식을 가정한다.

\[\begin{aligned} y = X\beta + \epsilon \end{aligned}\]

Linear Regression 에서 $\beta$ 에 대한 estimation 을 위해 Least Squares Estimation(LSE) 을 사용했었다.

\[\begin{aligned} \hat{\beta} = \underset{\beta \in \mathbb{R}}{\arg\min}\sum (y_i - x_i^{\top}\beta)^2 \end{aligned}\]

즉, $y_i-x_i^{\top}\beta$ 에 대해서 $f(u)=u^2$ 모양의 convex function 을 minimize 하는 방법, 혹은 이러한 function 을 $\beta$ 에 대해 미분한 식이 0이 되는 지점을 구하는 방식으로 estimation 을 하게 된다.

3. Quantile Regression

한편 Quantile Regression estimation 은 이러한 convex function 대신 아래와 같은 check function 이라는 녀석을 minimize 한다.

\[\begin{aligned} \rho_\tau(u) = u(\tau-I(u<0)) \end{aligned}\]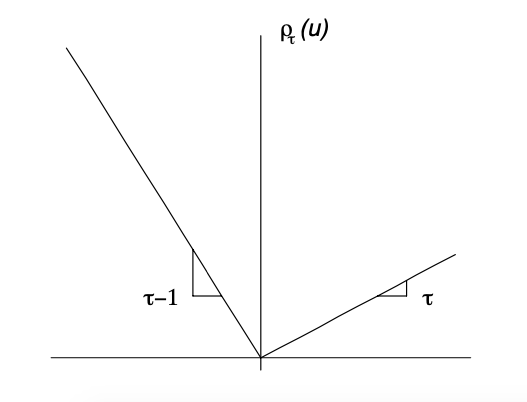

Quantile Regression 에서의 Estimated $\beta$ 는 아래와 같이 표현할 수 있겠다.

\[\begin{aligned} \hat{\beta} = \underset{\beta \in \mathbb{R}}{\arg\min}\sum \rho_{\tau}(y_i - x_i^{\top}\beta) \end{aligned}\]

위에서 말했듯, LSE 에서 minimum 을 구하고자 할 때는 objective function 을 미분해서 그 값이 0일 때를 구하면 됐었다. 마찬가지로 check function 도 미분해보면 아래와 같다.

\[\begin{aligned} \phi_{\tau}(u) = (\tau - I(u \le 0)) \end{aligned}\]

문제는, objective function 을 직접 미분을 하든지 check function 이 0인 부분을 찾든지, 둘 다 해를 찾기는 linear regression 보다는 쉽지 않다는 문제가 있다. 왜냐하면 objective function 이 딱 봐도 미분 불가능한 점 (바로 minimum이 있는 점) 이 존재하고, 그래서 derivative function 은 continuous 하지 않기 때문이다.

R 의 quantreg 에서는 objective function 을 minimize 하기 위해 Barrodale and Roberts Algorithm 의 변형된 버전을 default optimization method 로 사용하고 있다. 이외에도 함수의 옵션으로 optimization method 를 바꿀 수 있고, 많은 사람들이 check function 을 optimize 하기 위해 다양한 방법을 제시하고 있다. 내 논문의 simulation study 에서도 estimating 을 위해 check function 을 optimize 하는데 꽤 애를 먹었었다(사실 이 부분을 제대로 해결하지 못하고 논문을 끝맺어서 아쉬움이 남았다). 시간이 된다면 이러한 알고리즘에 대해서도 알아보고자 한다.